Table of Contents
Herman Haverkort > Recursive tilings and space-filling curves > Sound of space-filling curves > Sound of space-filling curves II
The sound of space-filling curves II
Proximity mapping: sonifying the landscape of locality-preserving properties of space-filling curves and permutation sequences
Sonifying locality-preserving properties
Computers often need to do computations on points in a grid. For example, when computing a weather map, the colour of each pixel of the map has to be computed. The order in which these pixels are processed can influence the efficiency of the computation. Ideally, the order is locality-preserving: that means that points that are close to each other in the grid are also close to each other in the order. However, this is not always possible. For example, in the figure on the left, the pairs of points marked in red are neighbours in the grid, but one of them is processed much later than the other. In the figure on the right, we also see such pairs, but the pattern is different: the times at which red points are processed differ, and the delays between neighbours are also different.
If I had not marked pairs of points with major delays between them in red, their locations would have been hard to spot in the figure. With high resolution grids of, say, 128 x 128 points, it would be even harder. To make it clear where the pairs of points with major delays between them are, we can visualize the processing order as a landscape: starting from a horizontal plane, we move each point of the grid up in a third, vertical dimension according to its position in the processing order:
Thus, the processing order becomes visible as a steadily ascending path, and pairs of points with long delays between them become visible as high, steep slopes. But what about processing orders for higher-dimensional grids? To show the pairs of points with long delays in a three-dimensional grid, we would need to create a four-dimensional landscape—which I cannot draw.
The goal of this project is to make the slopes of these undrawable landscapes hearable, in particular for processing orders of three-dimensional grids, and even higher-dimensional grids. The idea is that we process the points of the grid one by one, in the given order. When we process a point P, we also look at its neighbourhood, that is, the other points of the grid. If there are other points close to P that were processed much earlier, or will be processed much later, we create a sound. If the nearby point was processed long ago, we create a high-pitched sound; if the nearby point will be processed far in the future, we create a low-pitched sound. The longer ago, the higher; the further in the future, the lower. We construct these sounds for the neighbourhoods of all points of the grid, in the order in which they are processed, at high speed: in some of the examples below, we go through more than 40,000 points in about 100 seconds.
The result is a sound track in which low sounds indicate that we are approaching mountains that tower high above us in the four- or higher-dimensional landscape; high sounds indicate that we approach the edge of a cliff overseeing a valley far below. In other words, we hear how the space-filling curve bounces against its own earlier and later parts to fill the space. The sound track is polyphonic, because at any point in time, there may be cliffs and mountains on various scales in various directions. The overall trend in the sound track is that it rises in pitch. This is because initially, almost all points are still to be processed in the future, so only low sounds can be created, whereas eventually, almost all points will have been processed in the past, so only high sounds can be created. Alternatively, we can swap the roles of high and low and obtain a falling sound track.
This approach to sonify grid processing orders is one of several approaches I have explored. For the other approaches, please click here.
Math or music?
Below you will find thirteen sound tracks that have been generated from different processing orders for various grids. Depending on your background, you may find that the tracks violate many rules of musical composition and you may wonder why I did not correct those errors. Or you may feel that the tracks sound so musical, that this cannot be just the math at work: what you are hearing must be my own musical interpretation of the processing orders. Therefore, let me try to clarify what these tracks really are, and what aspects of the sound are actually under my control.
I did not compose any notes at all (it is better like that: I am not a composer). I created and ran a computer program that converts grid processing orders into sound, based on some basic parameter settings. I hope to publish a report later in which I explain the technical details, but for now: I would say these parameter settings are comparable to choosing, say, a photo camera's focus, aperture, shutter time, and film speed. But indeed, I also had an influence on the sound that goes a bit further than that.
First, I chose the processing orders to sonify. Tracks 2–7, 10, and 13 use processing orders that have been known in the mathematics and/or computer science literature for their technical merits. I selected these particular processing orders because I found that they sound interesting. I omitted other well-known processing orders (following a Hilbert or a Pólya curve, for example), because I found their sound tracks too chaotic: I could not find nice structures which I could focus my “sound camera” on. Tracks 1, 8, 9, 11 and 12 are created from simple variations on a well-known processing order. I designed these variations specifically in an attempt to create interesting sound tracks.
Second, I tried to control some aspects of sound colour, in particular the mix of overtones and formant strengths and frequencies. In Tracks 2, 3, 4, 8, and 13, I used different colours for different pitch ranges to make the sound tracks more transparent. Note, however, that my control of sound colour is limited. What sounds like a single note in a sound track, typically emerges from separate points in a traversal that goes through up to hundreds of points per second. It is still a bit mysterious to me what effects this has on the sound colour. In any case I cannot control the envelope (the development of sound over time) of the emergent apparent notes: the envelopes are determined by the processing orders that are sonified.
Third, I chose how exactly to map delays between pairs of nearby points to pitch. More precisely, at each point in the traversal of the grid, I calculate the relative times of all other points: their positions in the processing order relative to the current point. I map these relative times to pitch; loudness is determined by the discrepancy between the other point's relative time and its distance in the grid. With some processing orders, practically any value can appear as a relative time with high discrepancy. In such cases I chose a continuous mapping from relative time to pitch, so that the slightest variations in relative times can be heard, often as glissandos. In the case of Tracks 1, 3, 4, 9, 11, and 13, however, I found that a small set of different values for relative time dominated, and I decided to map the relative times to a set of discrete pitch values. In other words, I mapped the relative time values to a musical scale, which I tuned by hand. Thus I had some control over the harmonies and dissonances that appear. However, I always kept to the following rules: 1) the same relative time value always results in the same pitch; 2) higher pitch means further in the past (or, in a falling-pitch track: further in the future); 3) I try to make different relative times map to different pitch values on a chromatic scale. In practice this means that when I would try to get a particular note or chord at some point in the sound track, this would typically affect other notes and chords throughout the entire sound track—so tuning the scale is a complicated puzzle, and it is not like I can compose melodies just by tuning the scale.
As a post-processing step, I let some tracks fade out at, or sometimes before, the end.
Some explanation of the formulas and parameters behind all of this is available here.
Sound tracks
The sound tracks are quite different in style. You will probably like some of them more than others. I recommend listening to at least some parts of Tracks 1 to 9 to hear a more or less representative sample. Below the tracks are presented one by one. For all tracks at once, click here.
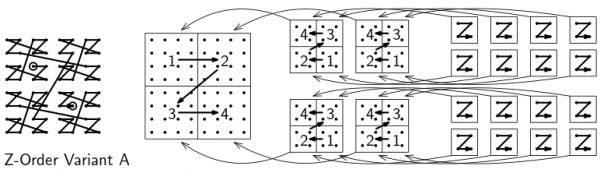
1. Z-Order Variation A on a three-dimensional grid
32,768 points at 114 points per second, cut after about 26,000 points, falling pitch
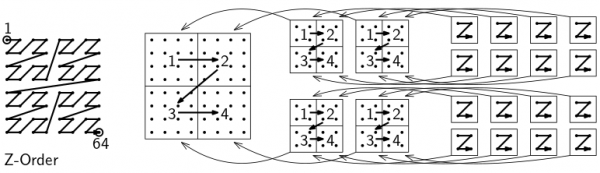
Z-Order is a processing order induced by a curve that was described by Lebesgue in 1904. It has been known in computer science at least since a report by Morton from 1966; therefore, numbering points in a grid in Z-Order is also called Morton indexing. Z-Order has many applications in improving the efficiency of computations. The figure below illustrates this processing order for a two-dimensional grid. The grid is subdivided into four parts, which are processed one by one, making a Z figure. Each part is again subdivided into four parts that are processed one by one, again making Z-figures. This subdivision procedure is repeated until we arrive at the level of single grid points. The figure illustrates the resulting order for a two-dimensional grid of 8 x 8 = 64 points.
For this harmonically interesting sound track I used a variation of Z-order for a three-dimensional grid in which the Z-figures are reversed on every second level of subdivision. In two dimensions, this would look like this:
The three-dimensional grid that underlies the sound track consists of 32 x 32 x 32 = 32,768 points.
2. Steinhaus-Johnson-Trotter algorithm for permutations of eight
40,320 points at 448 points per second, falling pitch
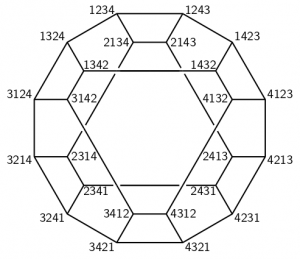
The sonification approach does not only work for regular grids, but also for permutations. A permutation is an order of distinct numbers. For the numbers 1 to 2, there are two different permutations (12 and 21); for the numbers 1 to 3, there are six different permutations (123, 132, 213, 231, 312, and 321). For the numbers 1 to 4, there are 24 different permutations, as follows:
In this figure, permutations that differ only by swapping two adjacent numbers, are connected by a line. Thus, the permutations also form some kind of grid. There are different methods to enumerate all permutations in such a grid, and they create different patterns of high and low sounds that are generated when nearby permutations appear much earlier or much later in the enumeration order. A famous algorithm to enumerate permutations is known by the names of 20th century authors Steinhaus, Johnson and Trotter. However, the algorithm has in fact been known since Stedman's 1677 book for its application in change ringing: varying the order in which to ring a set of church bells. With this algorithm, consecutive permutations differ only by one swap of adjacent elements. In other words, consecutive permutations are always immediate neighbours in our grid.
For this sound track (and also for the following two sound tracks) we apply the following twist to the processing order. Stedman's algorithm can be thought of as generating pairs of positions to swap. For example, (2,3) would mean: swap the 2nd and the 3rd number in the permutation. But what happens if we interpret (2,3) as: swap the numbers 2 and 3 in the permutation? We will sometimes jump from one point in the grid to another point that is not a direct neighbour. This sound track sonifies the locality-preserving (or locality-violating) properties of the resulting permutation enumeration method, going through all 40,320 different permutations of eight numbers. We hear a collection of falling glissandos.
3. Backtracking algorithm for permutations of eight
40,320 points at 420 points per second, rising pitch
This sound track is based on a simple algorithm to enumerate permutations that my academic father and I have been teaching in our algorithms classes for many years, because it is relatively easy to remember and easy to prove correct. Its locality-perserving properties appear to be very good, so, compared to the other sound tracks, I had to exaggerate the pitch differences a lot to make their structure noticeable. The structure consists of an interesting interplay of shifting rhythmic patterns, much unlike anything else in this collection.
4. Heap's algorithm for permutations of eight
40,320 points at 288 points per second, rising pitch
This sound track is based on an algorithm to enumerate permutations that was published by Heap in 1963. It appears to be the most efficient algorithm to enumerate permutations; however, it seems to be more difficult to understand and to get right than the previous algorithms. Its sound track distinguishes itself from the others in this collection by an unusually melodic bass line between 1/8 and 3/8 of the track's length, mirrored by a high-pitched melody in the last quarter of the track.
5. Mitchison-Durbin order on a two-dimensional grid
9,216 points at 184 points per second, rising pitch
In 1986, Mitchison and Durbin figured our how to enumerate the points in a two-dimensional grid such that the sum of the delays between all pairs of direct neighbours is minimised. But that does not mean that these delays are the same everywhere. This sound track sonifies the structure of their processing order on a grid of 96 x 96 points.
6. Z-Order on a seven-dimensional grid
16,384 points at 69 points per second, rising pitch
This sound track presents the locality-preserving properties of Z-Order on a seven-dimensional grid of 4 x 4 x 4 x 4 x 4 x 4 x 4 = 16,384 points.
7. Peano curve on a four-dimensional grid
6,561 points at 42 points per second, rising pitch
In 1890, Peano was the first to describe a true plane-filling curve. His curve is infinitely thin and infinitely crinkly and still it fills a square completely without jumping. When applied to a grid of appropriate size, it induces a processing order in which consecutive points are always immediate neighbours in the grid (note that with Z-Order, this is not the case). This sound track sonifies the locality-preserving properties of the Peano curve on a four-dimensional grid of 27 x 27 x 27 x 27 points. The climax is in the middle of the track, when we pass through the centre of the grid. Here the processing order squeezes itself in between points visited long before and points that are still to be visited far in the future; thus high tones and low tones are both strong there.
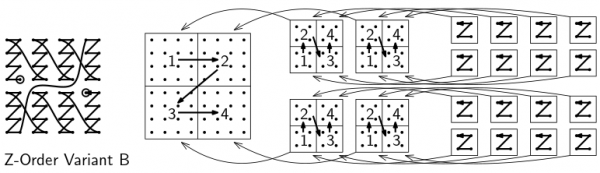
8. Z-Order Variation B on a three-dimensional grid
32,768 points at 126 points per second, rising pitch with marked jumps
This track sonifies a Z-Order variation in which the processing order is flipped inside the parts of the subdivision. The figure below illustrates the idea for a two-dimensional grid:
For this sound track, we apply the same idea to a three-dimensional grid. Note that this processing order (like most processing orders on this page) often jumps from one point to another point that is far away. This sound track also features a percussion sound effect that accentuates these jumps: the farther the jump, the louder the sound.
9. Z-Order Variation B on a five-dimensional grid
32,768 points at 81 points per second, rising pitch
This track is based on the same Z-Order variation as the previous track, but now on a five-dimensional grid. Whereas the previous track sounds a bit like a march, this one is more like a lullaby.
10. Meurthe curve on a three-dimensional grid
19,683 points at 36 points per second, rising pitch
The two-dimensional Meurthe curve was presented by Freek van Walderveen and myself in 2008 as a plane-filling curve that optimizes locality-preserving properties under certain technical conditions. This track sonifies the three-dimensional version of the curve. It is probably my personal favourite, even if it is a bit eerie: it is somewhat similar to Track 7, but it is richer, with longer and stronger melodic phrases that fit together well even though they do not adhere to any kind of musical scale.
11. Z-Order Variation B on a five-dimensional grid
32,768 points at 75 points per second, falling pitch
This track is based on the same processing order as Track 9, now with a different, falling scale and a different sound colour.
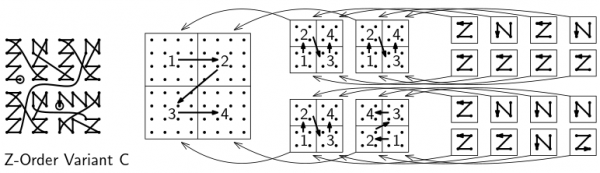
12. Z-Order Variation C on a three-dimensional grid
32,768 points at 120 points per second, rising pitch
Track 12 is the result of a conscious attempt to create a processing order that sounds musical. The other Z-Order variation tracks all sound a bit anti-climactic: in the last part, nothing new or surprising happens anymore and the tracks can barely (if at all) maintain their musical momentum. To counter this, I changed Variation B (from Track 8) into Variation C by making the last square (in three dimensions: the last of eight subcubes) similar to the curve as a whole, but reversed.
Since this change works on all levels of subdivision, this introduces a bit of variation on all levels, without creating chaos. Moreover, this change turns the end of the curve inwards: thus, at the end of the processing order, we process points that are relatively close to many points that were processed before. Thus, the sound track features an increasing number of high-pitched tones near the end and does not lose power.
13. Z-Order on a three-dimensional grid
32,768 points at 105 points per second, cut after about 26,000 points, rising pitch
The final track sonifies the original Z-Order in three dimensions, with a result that is quite similar to Track 1, maybe a bit less atmospheric and more plainly melodic.
All tracks at once
In one file:
haverkort_sound_of_space-filling_curves_ii_20211213.mp3
In separate files:
01-zordervara3d_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
02-sjtp8_haverkort_sound_of_space-filling_curves_ii_20211129.mp3
03-backtrackingp8_haverkort_sound_of_space-filling_curves_ii_20211129.mp3
04-heapp8_haverkort_sound_of_space-filling_curves_ii_20211213.mp3
05-mitchisondurbin_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
06-zorder7d_haverkort_sound_of_space-filling_curves_ii_20211213.mp3
07-peano4d_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
08-zordervarb3d_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
09-zordervarb5d-i_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
10-meurthe3d_haverkort_sound_of_space-filling_curves_ii_20211213.mp3
11-zordervarb5d-ii_haverkort_sound_of_space-filling_curves_ii_20211128.mp3
12-zordervarc3d_haverkort_sound_of_space-filling_curves_ii_20211213.mp3
13-zorder3d_haverkort_sound_of_space-filling_curves_ii_20211213.mp3
Audible properties of the processing orders
Above, I already made some occasional remarks about the relations between the traversal orders and audible features of the sound tracks. There are two more relations I would like to mention.
Self-similar structure
Many processing orders are defined recursively. For example, let's have a look at this figure again:
Here, a processing order filling a “unit” square is defined by subdividing the unit square into four subsquares, specifying which of these squares is visited first, second, etc., and finally, for each subsquare, specify how to rotate and/or reflect this subdivision scheme within that square. As a result, each subsquare generates exactly the same “base melody” that results from pairs of points that both lie within that subsquare. This is because both frequency and amplitude depend only on the distances between those two points in space and in time, but not on their location within the processing order and within the unit square as a whole. Differences in sound between different subsquares come only from the relations between pairs of points that do not lie in the same subsquare. Thus, we would hear the base melody four times, complemented with some voices that differ between iterations; for a three-dimensional processing order, we would hear eight repetitions—or, if the subdivision is based on dividing the cube into 3×3×3 subcubes—twenty-seven repetitions.
Because of the recursive structure, we may sometimes be able to recognise, during each of those parts, four (or eight, or 27) versions of that same base “melody” that are played four (or eight, or 27) times faster and with smaller pitch differences.
Palindromicity
Let's have another look at the first figure of this page:
The figure on the left shows a processing order as determined by Hilbert's plane-filling curve. We see that red pairs tend to come in sets of two, where every second pair in the set shows a smaller delay (time difference) than the first pair in the set. For example, among the pairs (2,15) and (3,14), the first has delay 13, whereas the second has delay only 11. More generally, when we refine the processing order recursively, we would find that the pairs come in sets of gradually decreasing delay. This is because the Hilbert curve is palindromic: as one travels along the boundary of one of the squares in the subdivision of the plane that underlies the curve, for example the vertical line that cuts the pairs (6,59), (7,58), (10,55) and (11,54), the signed time difference with the neighbouring point on the other side of that boundary always decreases. In the sound track, this results in pulses of rising pitch, that is, small glissandos, as we can hear here:
In contrast, in the figure on the right (Z-order traversal), pairs come in sets of constant delay: see, for example, (6,17), (8,19), (14,25) and (16,27). As a result, in the sonification (of a refined version) we hear pulses of constant pitch:
Thus, the sonification allows us to distinguish between palindromic and non-palindromic plane- or space-filling curves quite easily.