Laura Toma and I wrote a chapter on algorithms for elevation models (“Terrain modeling for the geosciences”) for the computing handbook set published by CRC Press in 2014. If you would like to read it, please mail me.

My remaining work on algorithms for elevation models concerns algorithms to compute optimal triangulations of the sea surface; algorithms to analyse the flow of water across a terrain, algorithms to compute visibility maps: which part of the terrain is visible from a given viewpoint? The odd one out (of which the applications are not restricted to geographical elevation data) is our paper:

• Fast generation of multiple resolution instances of raster data sets.
  By Lars Arge, Herman Haverkort and Constantinos Tsirogiannis.
  In Proc. 20th ACM SIGSPATIAL Int. Conf. on Advances in Geographic Information Systems (ACMGIS), 2012.
  text (or contact me for free access)

To be able to estimate the sea surface height in the past, we need to work with measurements from tide gauge stations located on the coast. We can triangulate the sea surface between these stations, and use the triangulation for interpolation. But what triangulation gives the best interpolations? For an answer, we look at recent times for which sea surface measurements from tide gauge stations and satellites are available, and we look for a triangulation that best matches those measurements:

• Minimum-error triangulations for sea surface reconstruction.
  By Anna Arutyunova, Anne Driemel, Jan-Henrik Haunert, Herman Haverkort, Jürgen Kusche, Elmar Langetepe, Philip Mayer, Petra Mutzel, and Heiko Röglin.
  To appear in Proc. 38th Symp. Computational Geometry (SoCG), 2022.

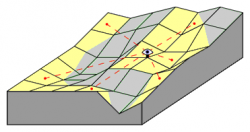
In hydrological studies we analyse the flow of water on a terrain, for example to study the effects of possible human intervention or to estimate risks of erosion. Assuming that flowing water always takes the way down that descends most steeply, we can predict the flow of water on a terrain from a digital elevation model. Thus we may try to compute, for every point (or river) q of a terrain, how much water flows to q, and where it comes from (the watershed of q). In principle, watersheds have a hierarchical structure: if water flows from p to q, then the watershed of p is contained in the watershed of q. Simple as it may sound, it is far from trivial to actually compute flow paths, watersheds, and their hierarchical structure. Some of the challenges, which we try to deal with in our work, are: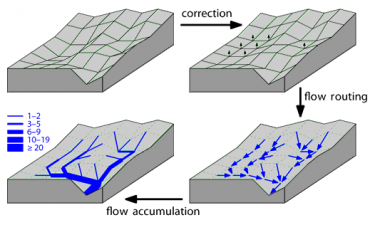

• the elevation models have limited precision, so that the direction of steepest decent is somewhat uncertain;
• in fact, due to measurement and sampling errors, digital elevation models tend to contain lots of places where the actual course of water seems to lead uphill, making it hard to guess the correct course from the model;
• tracing flow paths and watershed boundaries can take lots of computation time.

When analysing the flow of water across a terrain, represented by a digital elevation model, two main approaches can be distinguished. One approach treats the terrain as a continuous surface, of which the exact shape is estimated by interpolating between sample points for which an elevation is given. The other approach treats the terrain as a network of cells, in which each cell is treated as an atomic unit, and water that arrives in any cell continues its course down-hill to one or more neighboring cells.

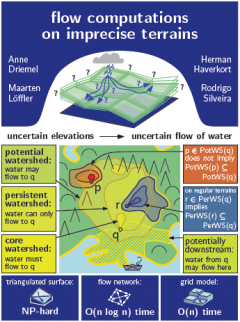• Flow computations on imprecise terrains.
  By Anne Driemel, Herman Haverkort, Maarten Löffler, and Rodrigo Silveira.
  Journal of Computational Geometry, 4(1):38–78, 2013.
  text

• Simple I/O-efficient flow accumulation on grid terrains.
  By Herman Haverkort and Jeffrey Janssen.
  In Abstracts Workshop on Massive Data Algorithms, 2009.
  Also available as volume 1211.1857 of Computing Research Repository (arXiv.org).
  text slides

• I/O-efficient hierarchical watershed decomposition of grid terrain models.
  By Lars Arge, Andrew Danner, Herman Haverkort, and Norbert Zeh.
  In Proc. 12th Int. Symp. on Spatial Data Handling (SDH), pages 825–844, 2006.
  text (or contact me for free access)

• Computing Pfafstetter labellings I/O-efficiently.
  By Lars Arge, Andrew Danner, Herman Haverkort, and Norbert Zeh.
  In Proc. Workshop on Massive Geometric Data Sets, number 02/05-I in technical reports of Münster University, Dept. of Computer Science, pages 37–41, 2005.
  text (This paper is on the same topic as the one above, but focusses on different aspects.)

• Flow computations on imprecise terrains.
  By Anne Driemel, Herman Haverkort, Maarten Löffler, and Rodrigo Silveira.
  Journal of Computational Geometry, 4(1):38–78, 2013.
  text (see also the image above)

• Flow on noisy terrains: an experimental evaluation.
  By Herman Haverkort and Constantinos Tsirogiannis.
  In Proc. 19th ACM SIGSPATIAL Int. Conf. on Advances in Geographic Information Systems (ACMGIS), pages 84–91, 2011.
  text (or contact me for free access)

• Implicit flow routing on terrains with applications to surface networks and drainage structures.
  By Mark de Berg, Herman Haverkort, and Constantinos Tsirogiannis.
  In Proc. 22nd ACM-SIAM Symp. on Discrete Algorithms (SODA), pages 285–296, 2011.
  text

• The complexity of flow on fat terrains and its I/O-efficient computation.
  By Mark de Berg, Otfried Cheong, Herman Haverkort, Junggun Lim, and Laura Toma.
  Computational Geometry, 43(4):331–356, 2010.
  text (or contact me for free access)

• Visibility maps of realistic terrains have linear smoothed complexity.
  By Mark de Berg, Herman Haverkort, and Constantinos Tsirogiannis.
  Journal of Computational Geometry, 1(1):57–71, 2010.
  text

• On IO-efficient viewshed algorithms and their accuracy.
  By Herman Haverkort, Laura Toma, and Bob Wei.
  In Proc. 21st ACM SIGSPATIAL Int. Conf. on Advances in Geographic Information Systems (ACMGIS), pages 24–33, 2013.
  text (or contact me for free access)

• Improved visibility computation on massive grid terrains.
  By Jeremy Fishman, Herman Haverkort, and Laura Toma.
  In Proc. 17th ACM SIGSPATIAL Int. Conf. on Advances in Geographic Information Systems (ACMGIS), pages 121–130, 2009. Winner of the best-paper award of the conference.
  text (or contact me for free access)