On this page we define some concepts to distinguish between different types of plane-filling curves, and illustrate them using plane-filling trails. In all definitions, we consider a plane-filling curve f, a real one, that is, without any jumps. Let f[a,b] be the image of the curve section from a to b, that is, U_{t ∈ [a,b]} f(t).

Some plane-filling curves generate trails that seem to consist of wide corridors, others squeeze themselves through infinitely narrow canyons or over infinitely narrow ridges or hillside trails. Formally, we can distinguish between plane-filling curves that are face-continuous and those that are not. The face-continuous curves are those for which the interior of f[a,b] is always connected. Narrow curves are those that are continuous but have sections whose images f[a,b] can be separated into two or more components by removing a single point. An example is shown in Figure 1a below: the arrows indicate some of the narrow spots where the curve squeezes in between parts of the plane that are visited earlier (lie lower) or later (lie higher). A curve section that starts just before such a narrow spot and ends just after, has an image whose interior consists of at least two components, which are separated from each other by the narrow spot.

The best-known plane-filling curves are self-avoiding: each time they touch a point that was visited before, they kind-of bounce off themselves immediately, or they squeeze themselves in between previous sections of the curve, but they never really cross a previous section of the curve. But some plane-filling curves cross themselves, such as the one shown in Figure 1b below. Since a plane-filling curve may be nowhere differentiable, we have to be careful with our definition of what constitues a crossing though. Let an (a,b)-loop be a simple closed curve (Jordan curve) g: [0,1] → R² such that g(0) = g(1) = f(a); g[0,1/2] ⊆ f[a,b]; g(1/2) = f(b); and g[1/2,1] ∩ f[a,b] = {f(a), f(b)}. We say that t₁, …, t₄ constitute a crossing of f if 0 ≤ t₁ < t₂ < t₃ < t₄ ≤ 1 and f[t₃,t₄] intersects the interior as well as the exterior of every (t₁, t₂)-loop.

Figure 1a: Dekking's curve is narrow.	Figure 1b: the Peano Railroads curve is self-crossing.

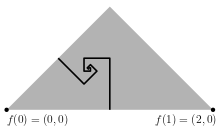Suppose f is the Pólya curve, and consider the point f(1/3) = (4/5, 2/5). The boundary between f[0,1/3] and f[1/3,1] is formed by two rectangular logarithmic spirals. One starts with a line segment from (1,0) to (1,1/2), the other one starts with a line segment from (1/2,1/2) to (3/4,1/4). Each spiral continues by alternating 90 degrees' turns to the left with further segments, where each segment has half the length of the previous segment. The spirals converge to f(1/3), but the direction from which they approach f(1/3) does not converge. Therefore, standing at f(1/3), it is undefined in which direction one should go to enter f[1/3,1]: if one picks any point f(t₂) with t₂ > 1/3 and moves from f(1/3) towards f(t₂) in a straight line, one always encounters a point f(t₁) with t₁ < 1/3 before reaching f(t₂).

Nevertheless, some plane-filling curves seem to be more crooked than others. I believe that in the case of the Pólya curve, one can always find a direction in which one can move some distance without encountering points that are very far away along the curve. More precisely, standing at f(t), one can always find, for any d, a point f(t₂) with t < t₂ ≤ t+d, such that for all f(t₁) on the interior of the line segment f(t)f(t₂) we have |t₁-t| ≤ d. Symmetrically, we can also find such a point f(t₂) with t-d ≤ t₂ < t. To put it differently, for any t and any d > 0, the boundary of f[t-d,t+d] is “unproblematic” around f(t), leaving at least some wedge into which one can move without having to jump over relatively high obstacles or relatively deep cracks. Let's call plane-filling curves that satisfy these conditions gentle. However, plane-filling curves that are not so well-behaved do exist: such curves may, for example have points f(t) where part of the boundary of a section f[t-d,t+d] resembles a fractal that spirals towards f(t). Let's call such non-gentle plane-filling curves crooked.

As an example, consider the two very similar curves in Figure 2. Each of them fills a fractal that remotely resembles a hexagon, tiled by seven smaller “hexagons”, that are visited one by one. At f(2/7) we find the point where the second, third, and seventh tiles meet; the curve leaves the second tile here and enters the third. Let's take f(2/7) as the origin of our coordinate system. The figures show a progression of views that zoom in onto f(2/7) in the following way: for zoom parameters ζ ∈ {1.0, 1.3, 1.5, 2.0, 3.0, 4.0, 5.0}, each point with coordinates (r cos φ, r sin φ), where r ≥ 0, is moved to (r^1/ζ cos φ, r^1/ζ sin φ). The vertical coordinates are treated in a similar way, and finally the image is scaled to fit inside the viewing window. The result is a distortion that magnifies the area around f(2/7) while ensuring that the points that lie on any line through f(2/7) remain the same.

ζ	Gosper curve	Inner-Flip Gosper curve
1.0
1.3
1.5
2.0
3.0
4.0
5.0
Figure 2: zooming in to see the crookedness of the Gosper curve

We see that in the first curve, the famous Gosper curve, the boundaries of the second, third, and seventh tile spiral towards the point where they meet. From geometric descriptions of the tiling¹⁾ it is not hard to see that the spiral is a logarithmic spiral (the growth rate is √7 per arctan √(3/25) ≈ 9⋅10⁷ per revolution, so the spiral would not be visible in any normal close-up view). As a result, every line segment between f(2/7) and a point in one of these tiles intersects points in both other tiles as well. Thus the curve is crooked. In contrast, in the second curve, the Inner-Flip Gosper curve, the boundaries between the tiles remain within narrow wedges and one can walk through f(2/7) from the second to the third tile without jumping over the seventh.