Table of Contents
Spherical Voronoi diagrams with Vorosketch
Vorosketch does not support input or output of sites on a sphere (yet). Nevertheless Vorosketch can generate Voronoi diagrams of points on the sphere, rendered according to one of various map projections, with the following work-arounds:
- random point sites uniformly distributed on the sphere can be generated with the -@ option;
- some pre-defined sets of sites (such as the corners of regular polyhedra and Tissot's indicatrix) can be generated with the -# option;
- user-defined point sites can be specified on the input in the usual way by giving their Cartesian coordinates (not their spherical coordinates) on the map of the chosen projection.
The catch with the sites generated with -@ or -# is that the sites themselves will not be drawn in the diagram, but you can see where they are if you draw contour lines with the -i option; see below for several examples.
Available map projections
To specify the projection, use -m “spherical(projection)”, where projection is one of the following.
| projection | parameter (α) | drawing area | standard parallel | properties | examples |
|---|---|---|---|---|---|
| orthographic | unit disk | 90N | -h | ||
| gnomonic | full plane | 90N | L-h | ||
| central azimuthal | |||||
| stereographic | full plane | 90N | CI | ||
| polar azimuthal | |||||
| azimuthal equal-area | unit disk | 90N | A | 20 sites | |
| lambert azimuthal | |||||
| azimuthal equidistant | unit disk | 90N | D | ||
| central cylindrical | strip [−1,1] × [−∞,∞] | 0 | |||
| mercator | strip [−1,1] × [−∞,∞] | 0 | C | indicatrix | |
| cylindrical equal-area | 1 | rectangle [−1,1] × [−1/(πα),1/(πα)] | arccos(√α) | A | |
| lambert cylindrical | |||||
| behrmann | 3/4 | 4 sites | |||
| gall orthographic | 1/2 | ||||
| peters | |||||
| equirectangular | 1 | rectangle [−1,1] × [−1/(2α),1/(2α)] | arccos(α) | ||
| gall isographic | √(1/2) | ||||
| sinusoidal | 2 | pseudo-ellipse with axes 2, 2/α | 0 | A | 4 sites |
| mollweide | 2 | ellipse with axes 2, 2/α | A | 20 sites | |
| hammer | 2 | ellipse with axes 2, 2/α | 0 | A | indicatrix |
| aitoff | 2 | ellipse with axes 2, 2/α | 0 | ||
| werner | heart shape with corners (0,0), (0,−1) | AD-f | 20 sites, indicatrix | ||
| stab |
Legend of properties:
| A | equal-area (shows sizes true to scale everywhere) |
| C | conformal (preserves angles) |
| D | equidistant (shows distances from the centre point true to scale everywhere) |
| L | preserves lines (shortest connections): great circles are shown as lines |
| I | preserves circles: all circles on the sphere are shown as circles on the map |
| -h | only shows one hemisphere |
| -f | slow implementation in Vorosketch: filter for pre-scan not yet implemented |
Pre-defined sets of sites
The sets of sites available with the -# option are the following:
| -# 2 | sites on poles: distance contours on parallels, bisector on equator |
| -# 4 | sites on corners of regular tetrahedron |
| -# 6 | sites on corners of a regular octahedron (on poles and on equator, spaced 90 degrees) |
| -# 8 | sites on corners of a cube (with Cartesian coordinates ±√(1/3)) |
| -# 20 | sites on corners of a regular dodecahedron |
| -# 24 | sites on equator: bisectors at meridians spaced 15 degrees' |
| -# 36 | sites on equator: bisectors at meridians spaced 10 degrees' |
| -# 62 | sites on intersections of parallels and meridians spaced 30 degrees (Tissot's indicatrix) |
Examples
Sinusoidal projection, 4 sites
The Voronoi diagram of four uniformly spaced sites on the sphere (four corners of a regular tetrahedron). Can you tell all regions are equal?
vorosketch -m "spherical(sinusoidal)" -p trubetskoy-modified -bi 0.07 -w 1.1 -\# 4
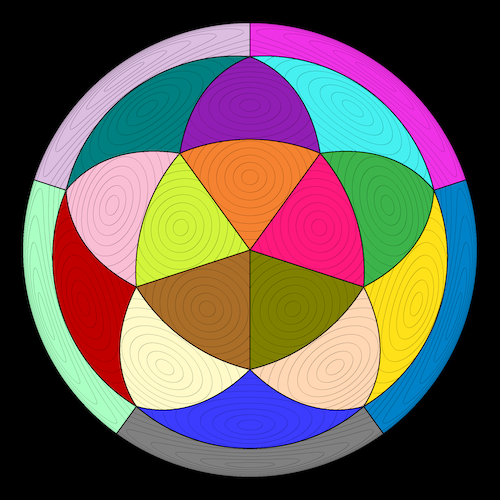
Behrmann projection, 4 sites
vorosketch -m "spherical(behrmann)" -p trubetskoy-modified -bi 0.07 -w 1.1 -\# 4
Azimuthal equal-area projection, 20 sites
The Voronoi diagram of twenty uniformly spaced sites on the sphere (the corners of regular dodecahedron, or, equivalently, the centres of the facets of a regular icosahedron):
vorosketch -m "spherical(azimuthal equal-area)" -p trubetskoy-modified -bi 0.07 -w 1.1 -\# 20
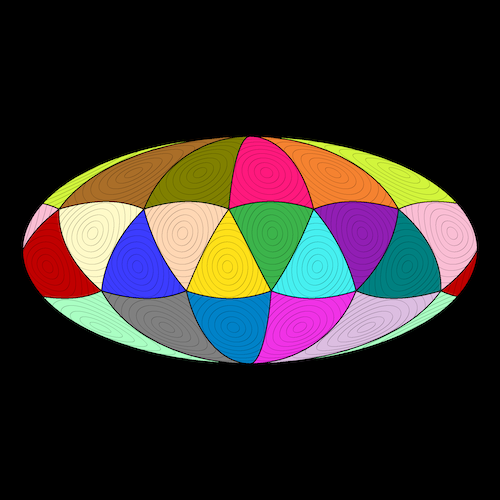
Mollweide projection, 20 sites
vorosketch -m "spherical(mollweide)" -p trubetskoy-modified -bi 0.07 -w 1.1 -\# 20
Stab-Werner projection, 20 sites
vorosketch -m "spherical(werner)" -p trubetskoy-modified -bi 0.07 -w 1.1 -\# 20
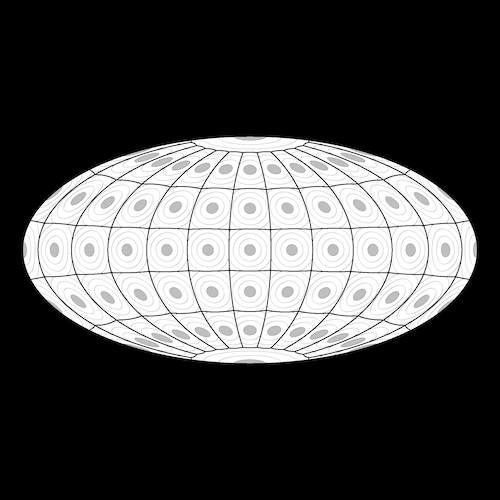
Hammer projection, Tissot's indicatrix
Below: Tissot's indicatrix for the Hammer, Mercator, and Stab-Werner projections. The distance measure includes subtraction of 0.07 so that around each site, we get a shaded disk (where distance is negative). Note that the sites of Tissot's indicatrix are not uniformly distributed on the sphere, so the indicatrix also has something of a distortion of its own. You may notice that the “parallels” do not look straight. That is because they are not actually parallels, but they are chains of Voronoi edges, each of which is a segment of a great circle, which a parallel is not (unless it is the equator).
vorosketch -m "spherical(hammer)-0.07" -i 0.07 -w 1.1 -\# 62
Mercator projection, Tissot's indicatrix
vorosketch -m "spherical(mercator)-0.07" -i 0.07 -w 1.1 -\# 62
Stab-Werner projection, Tissot's indicatrix
vorosketch -m "spherical(werner)-0.07" -i 0.07 -w 1.1 -\# 62
Page Tools
