Table of Contents
Herman Haverkort > Recursive tilings and space-filling curves > Sound of space-filling curves > Sound of space-filling curves I
The sound of space-filling curves I
Location mapping: sonifying the similarities between different parts of a space-filling curve
This approach to sonifying grid processing orders or space-filling curves is one of several approaches I have explored. For the other approaches, please click here.
For theoretical background on the approach demonstrated below, you might want to check out:
- The sound of space-filling curves.
By Herman Haverkort.
In Proc. Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture, pages 399–402, 2017.
text; full report (Aug 2017)
However, you may also simply start by having a look at the example sound tracks that are given below. Note that not all of these tracks are equally well-polished. Some are given her to demonstrate the potential of the approach, while others are given primarily for comparison or to illustrate open questions.
Two-dimensional location mapping
The sound track plays the above sketch vertex by vertex, at a leisurely pace of 75 beats per minute, so it is quite possible to follow the curve every step of the way while listening—try it!
| Every step… | means… |
|---|---|
| left up | voice 1 moves one step down |
| right down | voice 1 moves one step up |
| left down | voice 2 moves one step down |
| right up | voice 2 moves one step up |
Admittedly, this example is helpful to understand what is going on, but it this does not sound that exciting (see my report for a possible theoretic explanation). To get nicer sound tracks from space-filling curves, we can go in any of the following directions:
- alternate between sonifications of more detailed and less detailed sketches of the same plane-filling curve;
- add hand-composed voices;
- or use a completely different approach to sonify space-filling curves.
Alternating levels of detail
The following sample plays the Meander curve lot faster. In this track, all notes stem from the space-filling curve, but in different ways. There are three pairs of voices: a melodic pair, a rhythmic pair, and a “coarser” pair. The melodic pair plays the 27 x 27 grid of 729 notes, similar to the track described above, but now in reverse direction, and with different scales. The rhythmic pair has the same pitches as the melodic pair, but staccato, with dynamics controlled by the curve as well: the beats are stronger in the four corner subsquares out of the nine subsquares of any square (and recursively so). The coarse pair plays the curve at a slower sampling rate: effectively each group of 9 beats is merged into one chord with the pitch values of the 9th beat. The rhythmic pair of voices plays throughout the whole track; each melodic voice plays through most of the track but is sometimes replaced by the corresponding coarser voice.
| voice | pitch selection |
|---|---|
| 1 | C2 E2 F2 G2 A♭2 B♭(!)2 C3 E3 F3 G3 A♭3 B3 C4 D♭4 E4 F4 G4 A♭4 B4 C5 D♭5 E5 F5 G5 A♭5 B5 C6 |
| 2 | C3 D♭3 E3 F3 G3 A♭3 B3 C4 D(!)4 E4 F4 G4 A♭4 B4 C5 D♭5 E5 F5 F♯5 G5 A♭5 B5 C6 D♭6 E6 F6 G6 |
Three-dimensional location mapping
Here is an impression of the three-dimensional Meurthe curve as described here. It is 729 points of a 9 x 9 x 9 grid in 2 minutes, with some crescendo:
| voice | pitch selection |
|---|---|
| 1 | C3 D3 E3 G3 A3 B♭3 C4 D4 E4 |
| 2 | E4 F4 F♯4 G4 A♭4 A4 B♭4 B4 C5 |
| 3 | C3 B♭2 A2 G2 F♯2 E2 D2 D♭2 C2 |
Some more experimental examples can be found on a separate page. Another way to get three voices, is to sonify a two-dimensional curve on a grid of equilateral triangles using cubic coordinates.
Five-dimensional location mapping
Below are two renderings of Butz's five-dimensional Hilbert curve, sampled on a 4x4x4x4x4 grid, with a gradual crescendo and decrescendo. The sound track covers the 1024 grid points along the curve in 3.5 minutes. The first version sounds fairly gentle, the second is more adventurous.
In both versions, we can hear several characteristic properties of the curve. Here I will highlight only some of these. The curve fills 32 subcubes of a five-dimensional cube one by one. This results in 32 musical “blocks” of about 6 seconds each. These differ in how they are rotated in five-dimensional space: we can hear this in the music because the rotation determines which voice has which rhythm. In fact, only five different rotations are used. The first and the last block share the same rotation, and all other blocks appear in pairs that have one of the four remaining rotations. As a result, we effectively hear a short first block (6 seconds), 15 long blocks (about 13 seconds each), and a short final block. Every odd long block has the same rotation. These blocks alternate with the other 7 long blocks, which use the remaining three rotations: one of these is used four times, one is used two times, and one is used only once (in the central block), clearly marking the middle of the sound track.
| voice 1 | voice 2 | voice 3 | voice 4 | voice 5 | sound track |
|---|---|---|---|---|---|
| D5,C5,A4,G4 | C6,B5,A5,G5 | E3,D3,C3,A2 | C2,D2,F2,G2 | C4,B3,A3,G3 | |
| D5,C5,B♭4,G4 | C6,B♭5,G5,F♯5 | E3,E♭3,D3,C3 | C2,D2,F2,G2 | B♭3,A3,A♭3,G3 |
Four-dimensional location mapping
As described in my paper, there are theoretical considerations that suggest that three- and four-dimensional space-filling curves might have the greatest musical potential. Below is a first experiment in four dimensions: the “squared Hilbert curve” as described in my manuscript on higher-dimensional curves. Technically, it is obtained from the two-dimensional Hilbert curve as follows: consider the Hilbert curve as a mapping h from the unit interval to the unit square; now convert each two-dimensional point h(t) to a point with four coordinates by applying h to each coordinate of h(t). Thus we obtain a mapping from the unit interval to a four-dimensional cube, which turns out to have an interesting rhythm.
The sound track plays the 4096 points of a 8x8x8x8 grid in 14 minutes, simply the “raw” material, except for the automatic addition of dynamics. The dynamics are governed by the curve as follows: the music is softer when visiting points that are close to the starting point (by L1-distance in four-dimensional space), and louder when visiting points close to the second-last corner of the four-dimensional cube that is visited by the curve.
| voice | pitch selection |
|---|---|
| 1 | A1 B1 C♯2 D2 E2 F♯2 G♯2 A2 |
| 2 | C♯3 E3 F♯3 G♯3 A3 B3 C♯4 E4 |
| 3 | E4 F♯4 G♯4 A4 B4 C♯5 E5 F♯5 |
| 4 | G♯4 A4 B4 C♯5 E5 F♯5 G♯5 A5 |
Adding hand-composed voices
Adding hand-composed voices is, in a way, the least pure method of turning plane-filling curves into agreeable sound—and for me, not being a composer, it is also the most difficult and the least rewarding. It is particularly challenging because one is not given just one voice to find a harmonisation for, but two melodic voices that do not harmonise with each other particularly well to start with. Nevertheless, although I am not really satisfied with the results, I do feel that it worked out quite a bit better than I had expected to be possible a priori. So, for what it is worth, let me give you a few examples of what I managed to do with my limited musical skills—maybe this will convince you that these musical puzzles may actually be solvable and an able composer (like you?) could actually get it right.
Meander 4x4
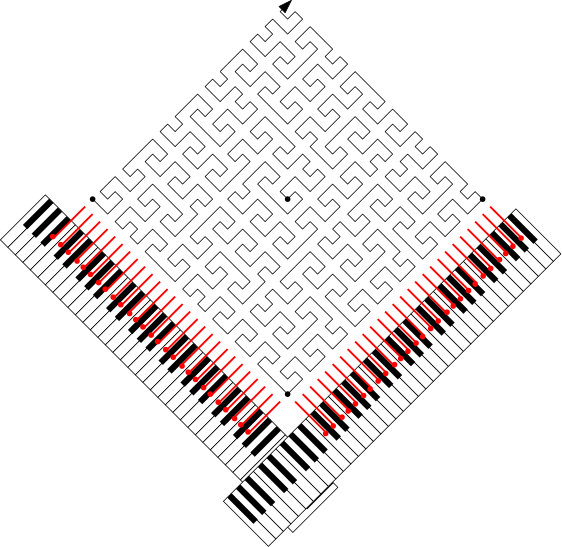
 Below is an attempt to create a “largo” from a space-filling curve. To get long notes, I used a Meander-like curve on a 4×4 grid, and I sampled it at a resolution of 16×16 (see figure). Each sample point sounds for 1.1 second. The melodic line of the second voice seemed to call for jumping down by a seventh instead of moving up by a second in “strategic” places, hence the non-standard selection of pitches. In the figure, the jumps are indicated by crossbars. Two hand-composed supporting voices are added below the two voices determined by the curve.
Below is an attempt to create a “largo” from a space-filling curve. To get long notes, I used a Meander-like curve on a 4×4 grid, and I sampled it at a resolution of 16×16 (see figure). Each sample point sounds for 1.1 second. The melodic line of the second voice seemed to call for jumping down by a seventh instead of moving up by a second in “strategic” places, hence the non-standard selection of pitches. In the figure, the jumps are indicated by crossbars. Two hand-composed supporting voices are added below the two voices determined by the curve.
| voice | pitch selection |
|---|---|
| 1 / horizontal axis (“flute”) | D4 E4 F4 G4 A4 B4 C5 D5 E5 F5 G5 A5 B5 C6 D6 E6 |
| 2 / vertical axis (“trumpet”) | B4 C5 D5 E5 F4(!) G4 A4 B4 C5 D5 E5 F5 G4(!) A4 B4 C5 |
Focusing on the technicalities of creating music from space-filling curves (and not on the obvious fact that I am not a trained composer), I am not quite satisfied with the result yet. Due to the space-filling character, all combinations of first-voice and second-voice pitch levels appear, and some of these are very dissonant (minor seconds). I did not manage to give all of these dissonances a proper place in the music. Possible solutions to explore:
- try other transpositions (maybe there is one where the dissonances are in less awkward places);
- try a hexatonic scale;
- try another curve, for example a curve that fills a triangle in a square grid (such as the Sierpinski curve) and position this triangle in the two-dimensional pitch space such that the second voice always remains at least a major second below the first.
Meander 3x3
One supporting voice starts with an intro of two alternating notes. After the primary voices start playing the curve, more supporting voices gradually join in. Dynamics and articulation are rudimentary. The vertices that are marked in the figure (at 1/4, 2/4, and 3/4 of the length) are also marked musically.
More location mapping
More experimental examples of sonifications through location mapping can be found on a separate page.